近代科学の成立過程９～商業簿記と利息計算から発展した代数学～

　前回（近代科学の成立過程８～近代の教育制度は西洋の商人がつくった算数教室から始まった）は、山本義隆氏の『十六世紀文化革命』から「第5章の商業数学と16世紀数学革命」の要約を引用しながら、この近代～現代の学校制度の原点は、特権階級の養成機関である大学が教会支配から金貸し支配に変わったことと、商業階級が建てた都市住民向けの算数教室であるということを見てきました。

【16世紀の代数学の発展に貢献したパチョリの算術大全】
　
　引き続き山本義隆氏の『十六世紀文化革命』から「第5章の商業数学と16世紀数学革命」中段部分の要約を引用しながら、数学の発展過程を見て行きたいと思います。
興味を持たれた方は応援もお願いします。

５ルカ・パチョリと『算術大全』　
　【修道士時代のパチョリ】
パチョリは数学に対してオリジナルな寄与をなさなかったけれども、俗語でかかれた彼の『算術大全（1494年）』は現存する知識の百科事典を提供し、16世紀の代数学の発展に貢献しうるようにしたのである。実際、パチョリの『算術大全』は商業数学から代数学まで複式簿記から幾何学までを記した、文字どおりの「大全」であった。
豊かな家庭の生まれでないパチョリは、商家に住み込み奉公に行った際、その才能を認められ家庭教師・貿易実務を行いながら学校で学び、その後、学業を続ける手段として1470年修道士となったのち、地位もないなか有力者や教皇の後押しもあって、1475年には大学で講義を行うまでになる。神学中心のパリ大学と異なり、イタリアの諸大学は創立以来、実学を比較的重視していたのである。
貧しい出自ながらレオナルド・ダ・ヴィンチといったルネサンスの第一級の明星たちと交わり、教皇やウルビノ公やミラノの君主といった聖界・俗界の権力者に庇護されたのは、時代の要請であった。あらゆる実際問題、あらゆる技術の問題の鍵は数学であると思える時代が到来していたのである。
数学は一方では美術や建築をふくむ技術の方面から、他方では商業サイドから強く求められていた。そして、一部の知的エリートのための書物ではなく、なによりも多数の商人や職人そしてその徒弟のための書物であった。実際、同著の中心は第2・3・4巻の商業数学にある。特に第3巻では世界ではじめて複式簿記（記帳を借方と貸方に表す方法）の記述・出版がされており、各国に翻訳され商業簿記の普及に多大な影響を及ぼした。（これはパチョリ自身の発明ではなく、ヴェネツィアの方法を簿記論としてまとめたものである。）
14世紀以来イタリアの諸都市の算数教室で使われていた教科書には、簿記や会計がまったく触れられていない。14世紀末から15世紀初頭にかけてしだいに整備されていった「商業簿記」は、商人の世界では実地で伝授されていたのであり、そのため多くの商人にとってはミステリアスだったとも言われている。口承される秘伝から公開された理論への転換が近代科学の幕開けを告げるのだとすれば、パチョリは簿記の技法を近代科学に押し上げた「会計学の父」となった。
パチョリ自身あくまでも貨幣経済と商業の世界の住人であり、商品経済は異質な商品の価値（交換価値）を貨幣により一元的に数量化する。簿記論の第八章でパチョリは、商品支払いに際しては「交換に渡した商品の細目を数量・重さ・尺度・１ブッシェル・１ポンドあたりの値段等を特記しなければならない」と書き記し、「私は自分の言わんとすることを数量と重さと尺度を用いて表現し」と語った統計学の創始者、17世紀イングランドのウィリアム・ペティの科学思想を先取りしていたのである。
この時点の最先端であるパチョリの方程式論は、（複式簿記の発想に立ち）負数係数や負数解を認めておらず、高次方程式もまた「不可能」と記されていた。その後の方程式論の発展は、記号の導入とともに、数の範囲を負数、虚数、複素数へと拡大してゆくこと、そして三次方程式の一般的な解法を見出すことに求められたが、その出発点はパチョリのこの問題提起にあった。

　
【方程式のはじまり】
　パチョリは負数・ゼロを独立の数として認めていないので、負数係数の方程式は考えられていない。すなわちこの時代の方程式には現代の教科書にみられるようなAx^2+Bx+C=0のような等号の一方が０となる形の方程式は決して現れなかったのである。
　
＜当時の表記の方法＞
　貸方（正の値）　　借方（正の値）
　　Ax^2+Bx　　＝　　　C
　
等号の両側は必ず正の量であければならず、その基本的な考え方は、現金と商品の変動を借方勘定と貸方勘定の二通りに把握して左右に書き込み、トータルで左右が均衡しないければならない複式簿記の発想が原点にあることを示している。
すなわち、方程式とは複式簿記をもとに発展したものであると考えられる。
　
　

６ニコラ・シュケーとフランス代数学の始まり
イタリアに比べれば多少遅れているにしても、15世紀にもなれば商業は北ヨーロッパでの諸都市でも大きく発展していたのであり、商業算術はインド・アラビア数字とともに浸透していた。
フランスは農耕社会の要素をおそくまで残していたが、イタリアの影響下にあったリヨンは大市（賃借清算や為替決済が行われる「信用の大市」のこと）開催権が付与されていた。「そこではすべての貨幣・為替が流通する。期間中リヨン滞在が許され、税は免除、為替・銀行業務を営むことができる」のであり、国際的な両替・賃借契約清算事務の行われる取引所として栄えていた。
ここリヨンにおいて「フランス代数学の父」と呼ばれるニコラ・シュケーが1484年（パチョリの『算術大全』より10年早く）に『数の科学における三部分』を書き上げる。
リヨンは印刷出版都市でもあり、16世紀を迎えると算術・簿記・利子計算など商人むけ実用書のジャンルでは、リヨンの独断場であった。シュケーが関心を寄せていたものもまた商業数学だった。
シュケーの書籍の注目点は、それまでの「修辞代数」から「記号代数」への転換点に位置していることにある。その中で彼は、0及び負の整数を考え、方程式の係数及び解に負数を認めたのである。それを「負債」と位置付けられ、数学が商業の枠組みで理解されていたことを示している。「算術ないし代数の計算が発展したのは、実用的な問題に関してである。複式簿記だけが負数の観念を提供することができた」のである。シュケーは複素数解になる方程式についてはなお「不可能」としているが、しかし彼による代数の記号化の開始と負数の導入は、代数学を大きく前進させるものであった。
いずれにせよ注目すべきは、のちにヴェエトからデカルトそしてフェルマらによって近代代数学が発展させられるフランスにおいても、代数学が商業数学に端を発し、大学アカデミズムの外部で形成され、当時の非学術言語であるフランス語の書籍により著述されていたという事実である。
　
　
７．ドイツとオランダのケース　
　
　中世後期からルネサンス期にかけての商品経済の浸透が人間活動の諸側面の数量化を促し、算術の普及に寄与したことは商業以外の場面でも顕著である。認識における定量的測定の重要性の提言が、プラトンやピュタゴラスの影響によるだけではなく、それ以上に商品経済の発展に促され貨幣経済の浸透に触発されたものであることが、市場の喧騒と該当の雑踏の中にこそ新の知が見出されるというクヌーザスの言葉にも表れている。
クヌーザスにあっては現実認識にたいして数学的方法が不可欠なものとみなされるのである。彼の『精神について』には「私たちの精神による理解の範型は数である。数がなければ、比較も認知も区別も測定もありえない。数がなければ事物の他の事物と区別される形での認識はありえない」と記されている。
現実にもクヌーザスはそれまで、天文学でしかおこなわれていなかった定量的測定を地上の科学に押し広げ、それまでの受動的な観察にもとづく定性的な「自然哲学」から能動的な側手にもとづく定量的な「自然科学」への転換を予言することとなる。
ボヘミヤやザクセンの鉱山地帯での試金においても精密な測定が重要視されていたこと、またその世界において十進計量システムが考案されていたことはすでに扱ったが、それは貨幣経済の発展がもたらしたものであるが、正確な測定は貨幣や貴金属にたいしてだけ重要なわけではなく、商品経済が発展するかぎりで、すべての商品にたいして要求されることになる。実際、中世後期には「販売は製造と同様に監督され、商人は良き分銅と天秤を備え、秤は検査対象として管理されていた。」とある。
そんなわけで、ドイツ諸都市においても、14世紀以降、商人の子弟のために俗語で教育する「習字学校」が形成され、ドイツ語の読み書きと初等算術が教えられた。ハンザ同盟を中心にして商業が大きく発展していた北海・バルト海沿岸地方だけではなく、鉱山業で栄えていた中央ヨーロッパの諸都市においても算術教育の必要性は高まり、15世紀末以降16世紀にかけて「算術教師」によっていくつもの俗語の算数書がかかれることになる。
この時代の商業のいまひとつの中心地としてネーデルランドが挙げられる。その南部は国際的な商業の中心地としてイタリアとならぶ繁栄を誇っていた。とりわけプリュッヘ（現ブリュージュ）は、13世紀以降、イングランドの羊毛、フランス及びライン沿岸のワイン、そして北欧やロシアからもたらされる木材、小麦、毛皮の集散地として栄え、14世紀にはヨーロッパのもっとも重要な金融市場の一つとなっていた。しかし、15世紀末にはブリュッヘの繁栄は終わりを告げ、商業の中心はアントウェルペンに移動する。アントウェルペンはイングランドの毛織物や東洋からの商品―インド航路を開いたポルトガルがもたらす香料―の大陸への入り口でもあれば、南ドイツの銀と銅の集散地でもあり、ヨーロッパ随一の国際貿易港にのし上がっていた。

【アントウェルペン・ハンザ同盟商館】
そんなわけで、ネーデルランドにおいても、16世紀には俗語の算術書の出現を見ることになる。いずれにせよ、16世紀前半のネーデルランドにおいても「数学学習」にむけての主要な推進力は、ますますもって商業の直接的および間接的な必要性に由来しているのであり、そして成長する都市の要請にもとづいていたのである。とりわけ、幾何学における相対的な停滞と対比される算術書出版の増加は、この時代における商業サイドからの圧力がいかに数学の発展に強力に作用したかを、あらためて示している。
16世紀イタリアにおいて方程式論の飛躍的な発展を見るが、その土台は、このような西ヨーロッパにおける商業数学の普及にあった。すなわち「代数学の勃興を惹き起こすものとなったきっかけは、イタリアのロンバルディア、北ヨーロッパ、あるいはレパントなどの銀行家や商人の会計室における、きわめて卑俗で功利的な要求だった」と言える。

【数学至上主義】
　クヌーザスが現実認識に対して数学的方法が不可欠であり、「私たちの精神による理解の範型は数である。数がなければ、比較も認知も区別も測定もありえない。数がなければ事物の他の事物と区別される形での認識はありえない」と記したように、この時代は市場社会の拡大を契機に定量的測定や通貨換算のための一元的数量化及び商業数学の発達につながり、代数学及び近代科学の発達につながってゆくことになる。
貨幣経済が浸透する中で、市場拡大→私権欠乏拡大→あらゆる物が商品化→すべて通貨換算し数量化されていった時代である。
その延長線上で商品やサービスに限らず人間社会の全ての事象が数で表すことが出来るという正当化観念を生み出すきっかけともなったのである。
まさにあらゆる実際問題、あらゆる技術の問題の鍵は数学であると思える時代といっても過言ではないだろう。
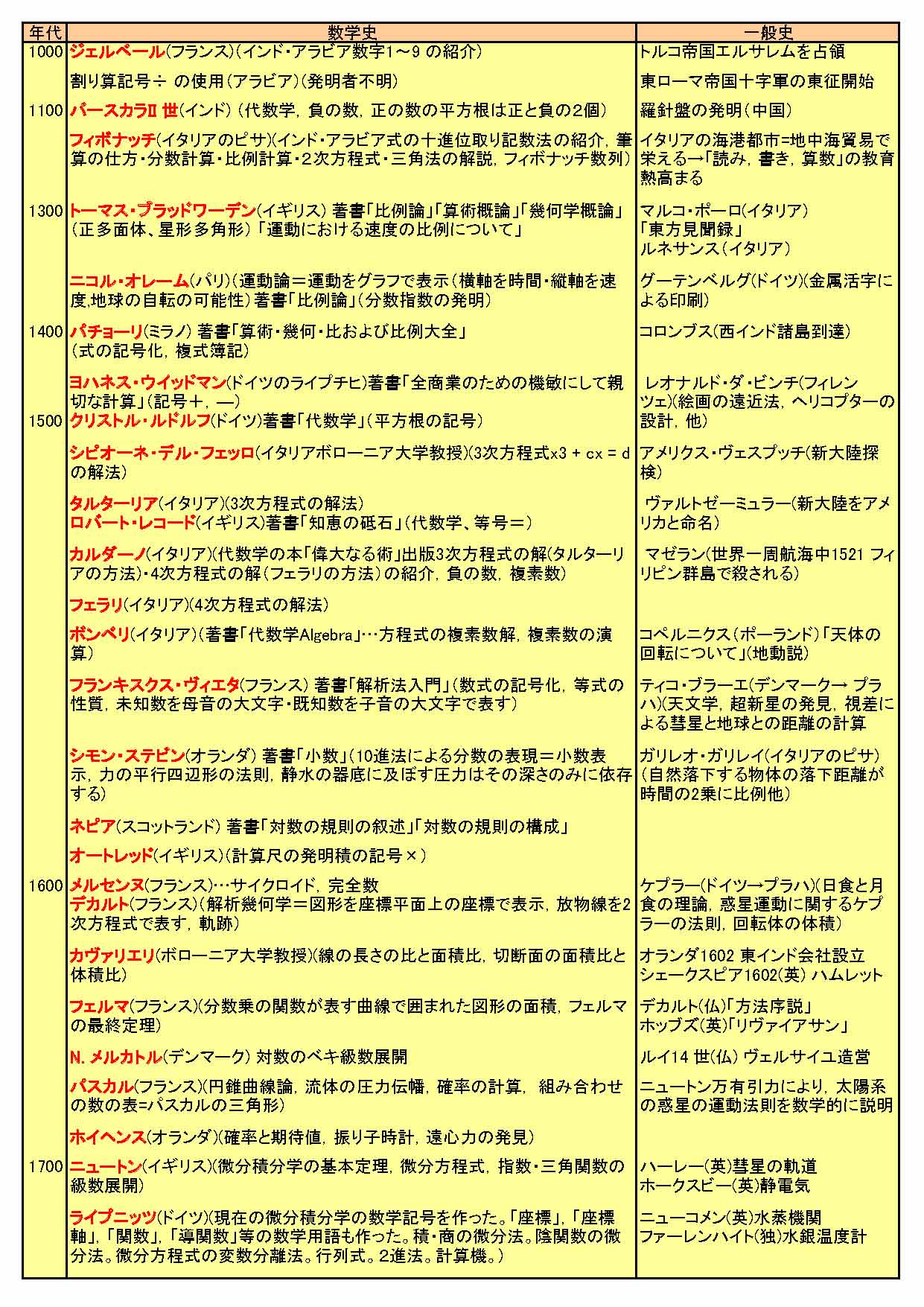
（下図数学史年表参照。16世紀以降自然現象をも数学で表現する物理法則等が発表されてゆくようになる。）

　
　
【銀行家や商人の卑俗で功利的な要求→複利計算から代数学が発達した】
　幾何学の面積計算では２次方程式、体積計算でも3次方程式までしか必要とされないが、この時代から高次方程式論が研究され、商業数学から代数学へ発展し始めたのは、なぜか？
銀行業務上の利息と収益を把握するために複利計算を行う必要性があったのからではないだろうか。
複利計算のために高次方程式論が必要とされた。
いわば金貸しが利益を生み出せるように、高次方程式→代数学が発達したということである。
　数理的理論での経済予測や確率論を利用した金融工学など、現在の市場社会にも通ずるものがこの当事から見られたのである。現在における経済学の土台が生まれたのではなかろうか。

【当事の商業都市】
　商業簿記から発展した代数学ではあるが、実質的には、市場拡大→私権欠乏拡大が原動力となり、他の科学技術と共に発達していったのが実態である。
次回は、引き続き『十六世紀文化革命「第5章の商業数学と16世紀数学革命」』から15世紀以降、数学発展の真相に迫っていきたいと思います。

Tweet

List　   投稿者 pandaman ｜ 2011-12-06 ｜ Posted in 13.認識論・科学論 ｜ 5 Comments »　

トラックバック

このエントリーのトラックバックURL:
http://blog.nihon-syakai.net/blog/2011/12/2162.html/trackback

コメント5件